問題分析、基本テクニック
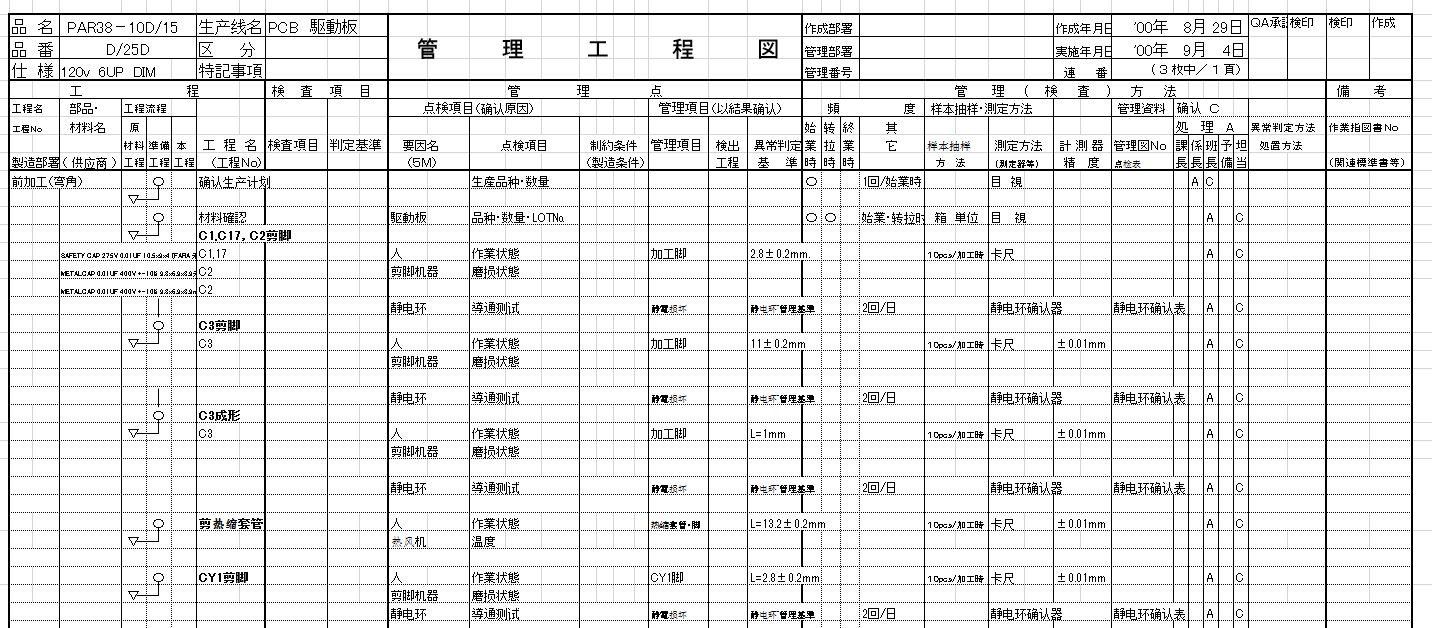
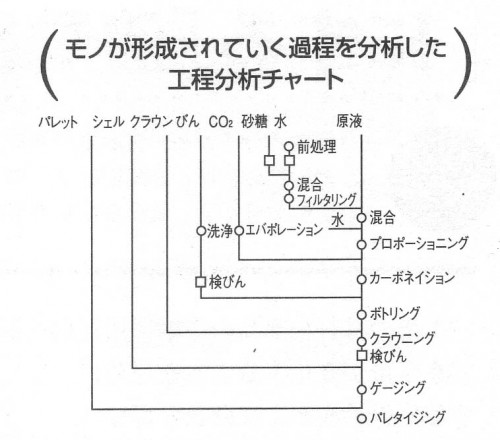
工場で製品がどのように組み立てられていくのか、人がどのような手順で仕事をしているのかなどモノの流れや作業の流れを明らかにする分析テクニックが工程分析です。
工程分析には分析対象によって製品工程分析、作業者工程分析、連合作業分析、サーブリック分析、事務工程分析など、多種ありますが、どの分析でも基本となる考え方は「対象の流れを要素に分けてその要素の前後関係を明らかにする」ということです。
工程分析では原則として前要素から後要素へ矢印で結ぶ表現をとります。
工程分析の目的にひとつは流れの中で問題部分を明らかにするということです。
製品が作られていく工程であればボトルネックとなっている工程、仕掛材料が多い工程等の問題を明らかにします。
2つ目の目的は工程の流れの改善、再設計時のシュミレーションです。
また、平面上あるいは空間的にどのようにモノが流れているかをうまく表現する場合には流れ線図(ストリングチャート)が有効です。
流れ線図では線はモノや人の動く経路ですので「動線」と呼ばれます。動線が密集している部分やほとんど動線のない部分がすぐにわかりますので、レイアウト設計などに有効です。 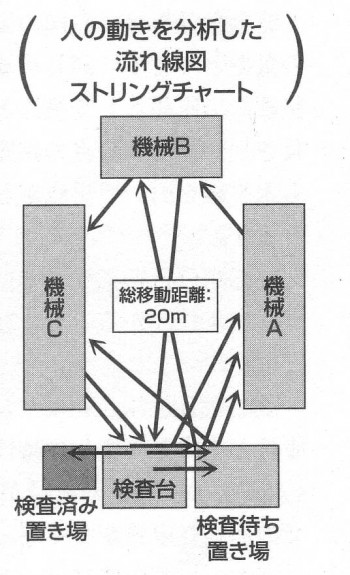
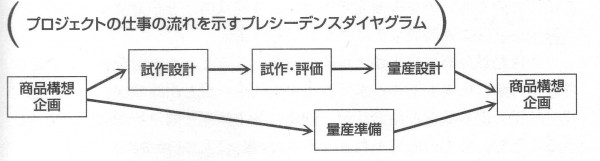
さらにプロジェクトの仕事の流れを示す手法として、プレシーデンスダイヤグラムやアローダイヤグラムなどが使われます。これらはネットワーク分析とも呼ばれプロジックトの期間短縮を検討する場合に用いられます。
ネットワーク分析では全体の時間的な長さ(期間)を決定づけられている一連の要素のつながり(一般にクリティカルパスと呼ばれる)を容易に見出すことができます。
ポイント ①要素の前後関係を矢印で結ぶことが可能。
②モノや人の流れには工程分析図、流れ線図を使う。
③プロジックトの流れにはプレシーデンスダイヤグラムを使う。
流動数分析
流動数分析工場の材料や部品の在庫、店舗の在庫のように入庫と出庫によって在庫量が変化するような対象に対して、時系列での量の変化を明らかにする分析手法が、流動数分析です。
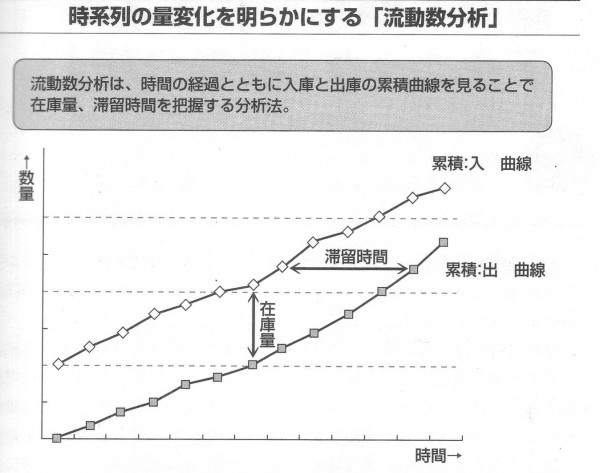
流動数分析は下図のように横軸に時間の経過をとり、縦軸にモノの量をとります。
同じグラフ上に入庫量の累積線を入庫線、出庫量の累積線を出庫線として描くとある時点での入庫線と出庫線の差(垂直線の長さ)がその時点の在庫量を表します。
また、ある時点の入庫線の点から水平線を引いて出庫線と交わるまでの長さがその在庫の滞留期間になります。
流動数分析のグラフでは入庫と出庫の周期性や在庫量の変化状況がビジュアルにわかるので在庫回転数の向上や在庫量の低減などの問題解決でよく用いられます。
流動数分析は結果としての在庫量でなくそれを決定づけている入庫量と出庫量の変化の特性(周期性)に着目して安全在庫量や最適発注(入庫指示)方法の検討が行われます。
安全在庫量とは次の入庫機会までの間に在庫量がなくなってしまう(欠品)ことがないような在庫量のことです。
入庫方法にはダブルビン方式、定期発注方式などがあり、どの方式でどのくらいの量を補充するのがより経済的かを検討するときのシュミレーションに流動数分析がよく用いられます。
この流動数分析は需要と供給のバランスをとりたい対象であればさまざまな対象に応用することができます。
入庫状況、出庫状況、入金状況と出金状況、到達状況と出発状況、問題の発生状況と解決状況などに置き換えることで、多くの応用が利きます。
ポイント ①流動数分析から在庫量の推移、在庫滞留期間がわかる。
②流動分析は在庫回転数の向上m在庫低減などの目的で使う。
③流動数分析は安全在庫量や最適発注方法の検討がしやすくなる。
生産現場で作業者がどのような作業にどれだけの時間を使っているかなどを調査、分析する手法が稼動分析です。時間の使われ方を明らかにする分析テクニックです。
稼動分析は大きく2つの方法があります。1つは分析対象を連続的に見て状態を記録する「連続観測法」です。もう1つは対象を連続的に観測するのではなくランダムに観測タイミングを決めてそのときに対象がどのような状態であったかを記録し、その集計結果から稼動状況を推察する 「ワークサンプリング(WS)法」です。WS法ではある設備について数日間にわたり ランダムに延べ1000回の観測をしたところ、250回が稼働中という結果が出れば稼働率を25%程度と判断します。
以前は連続観測法とWS法は対象を直接観測する方法しかありませんでしたが、最近はVTRで記録して後で分する方法をとるようになってきています。
稼動分析は時間に比率を明らかにする手法ですので、その表現方法は量を比較して見やすい円グラフや帯グラフ(構成グラフ)を使います。
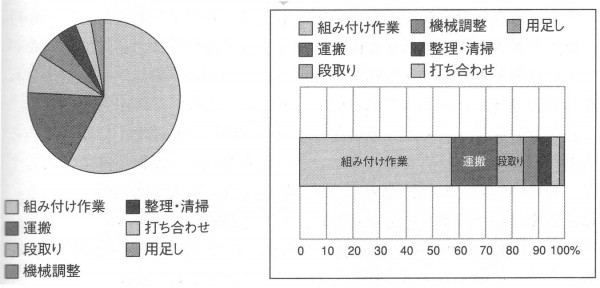
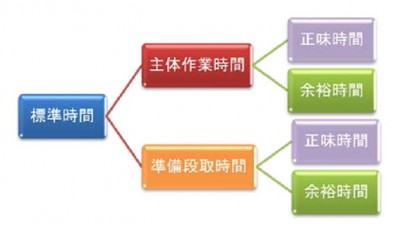
稼動分析に限りませんが分析は分析することが目的ではなく、なんらかの問題解決、改善が目的です。したがって、稼動分析における要素分析は分析後の改善実施の仮説に基づいて決めます。
たとえば、下図のように稼動分析した結果、「段取り、準備作業」の時間比率が多いことがわかったなら、「なぜ段取り、準備作業の時間が多くなっているのか」「具体的にはどういう段取り、準備作業が発生しているのか」を知るために、作業を再度、調べなおすことになります。
このような2度手間を防ぐためにWS法では予備(予行)調査を行って項目要素の適正化を 行った上で、本調査を実施するのが賢明です。
ポイント ①対象を連続的に見る手法が「連続観測法」。
②対象を時々、見る手法が「ワークサンプリング(WS)法」。
③分析の要素分類は、改善仮説に基づいて設定する。
原因分析
問題解決において、解決しようとしている問題がどのような原因によって生じるかという分析はよく行われます。
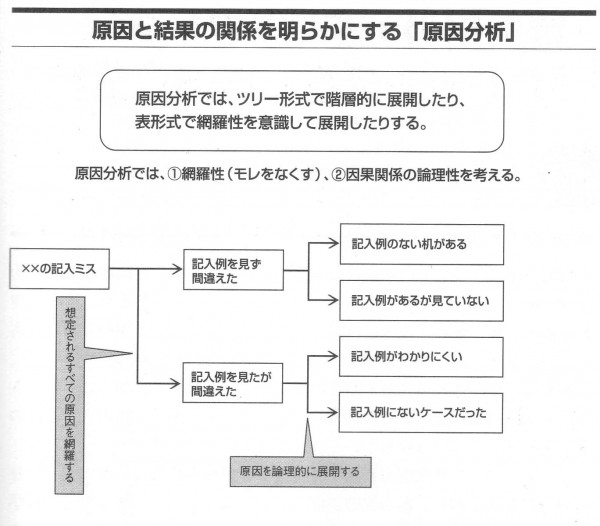
問題の原因分析は一般に下図のように左から右に向かって、あるいは上から下に向かって結果→原因の順に展開していきます。
その際、原因の考察を何回にもわたって多段階に深堀りするのがこの分析の鉄則です。問題解決能力の高い組織では「なぜを5回繰り返せ」と言われたりします。
原因分析は分析の形式としては非常にシンプルであるために、実務としては軽視されがちです。しかし、実はシンプルな原因分析に手間をかける意義は想像以上に大きいのです。
人間は問題の原因とその対策を考える際、簡単に思いつく原因や対策が打ちやすい原因を考えてしまし他の原因要素に思考が及ばないことが多々あります。
そのため、考えモレの原因に対してアクション起こせず、問題解決の効果が狙ったとうりに出ないことがあります。
このような事態を防ぐために、頭の中だけで考えず、あえて手間をかけて原因を書き出す、それも多段階に展開する原因分析は非常に有効なのです。
原因分析は「他の原因は考えられないか」「その原因を生んださらなる原因は何か」をあえて書き出して考えるところに意義があるのです。
原因分析を行うことで、原因要素がループ構造(悪循環)になっていることが認識できる場合があります。そのような原因の悪循環構造に対しては対処治療法的に原因の要素に対策を打つより、悪循環を断ち切る 、あるいは逆循環になる対策を考える必要があることがわかります。
なお、原因分析の中には下図のFMEA(故障モード影響分析)のように原因から予想される影響を考える手法もあります。
ポイント ①多段階にわたって何度も原因を考える分析法
②原因要素の悪循環構造を断ち切る方法
③原因から影響を考える際にも有効
パレート分析、ABC分析
自社の顧客を売上高の多い順に棒グラフで並べると下図のように約2割の顧客で約8割の売り上げ比率を占めていることがあります。
また、自社の費用を額の多い順に並べると約2割の費目で約8割の費用額を占めていることもあります。
あるいは製品の品質不良の原因を調べると2割の原因で全体の不良の8割をしめていることがあります。
さらにイントラネット上の掲示板への書き込み状況などにも、全体の2割の人で全体の発言量の8割が占められるという特性があるようです。
このように2割程度の要素で発生量の8割を占めることが我々の身の回りにはよくある種の法則のように思えます。
イタリアの経済学者パレートが人々の所得分布を調べ全体の2割の人で8割の所得額を占めていることを発見したことからこのような特性は「パレートの法則」と呼ばれています。
パレート分析は発生量が多いものをA区分、中くらいのmのをB区分、ほとんど発生していないものをC区分 と分けることから別名ABC分析とも呼ばれます。
問題解決においても多くに検討対象について同じ程度のパワーをかけるのではなく、検討対象を絞り込むつまり重点化をして検討することは重要です。
非常にシンプルな方法ですが発生量の多い順に棒グラフの項目を並べ替えて表現し直すパレート分析が重点化 テクニックの基本となります。
稼動分析、原因分析の結果をパレート分析することでどの要素に重点化して検討すればいいのか、その共通理解を得ることができます。
要素数が2桁(10以上)ならば必ずこのパレート分析をして対象の重点化を行うようにすべきです。
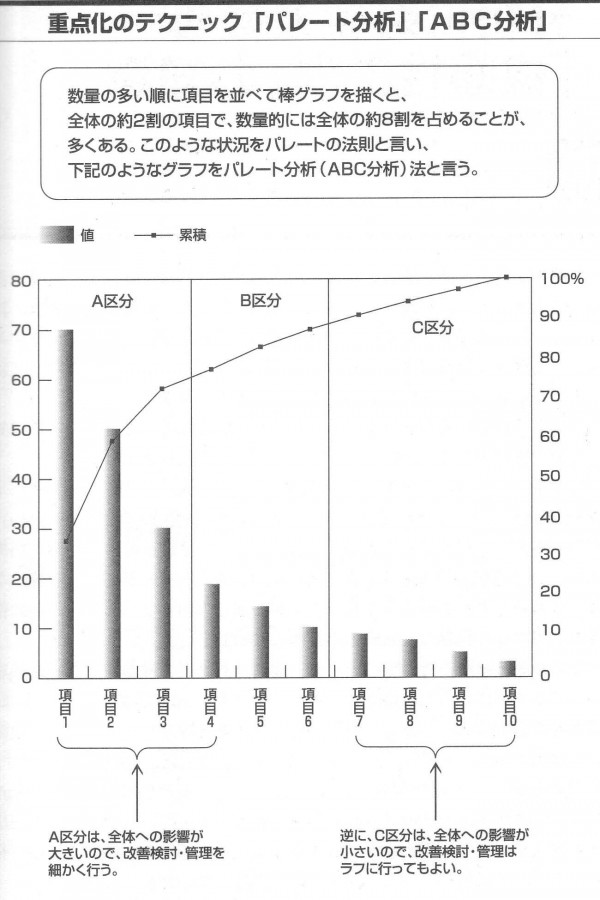
ポイント ①2割-8割の法則 (パレートの法則)は広くあてはまる。
②自明なことでも、認識の共通化のために重点分析を行う。
③稼動分析や原因分析の結果を重点化するとより分析が活きる。
信頼性工学知識
各種の製品、部品、システムは初期不良もあれば使用中に故障する場合もあります。故障時に新しく入れ替えたほうがいい製品もあれば、修理をしながら使用していくほうが いい製品もあります。
また、故障をすると大きな悪影響を及ぼすシステムもあり、そのようなシステムに対しては故障しないように事前に予防対策をとる必要があります。このように対象の使用可能性、信頼性、保守性などを検討する際に知っておく必要がある知識として「信頼性工学」があります。
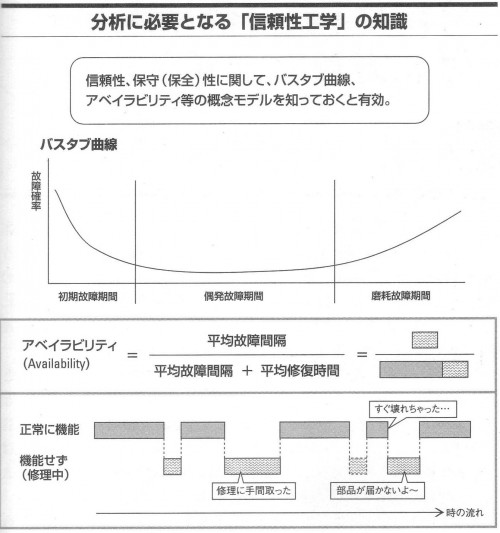
信頼性工学ではバスタブ(Bathtub)曲線、リライアビリィ(Reliiability)、アベイラビリティ(Availability) 保全性(Maintainability)平均故障間隔(MTBF:Mean Time Between Failure)平均修理期間 (MTTR:Mean Time To Repair)をはじめ、下図のような特殊な概念があります。
このような概念モデルを知っておくと、工場などの設備管理上の問題を整理し分析するときに有効です。製品の故障確率の時間軸の分布は縦軸に故障率、横軸に時間の経過をとってグラフにすると下図のようになります。
この故障率のグラフは形が西洋浴槽に似ていることからバスタブ曲線と呼ばれています。製造開始の初期は初期不良・初期故障(Initial failure)期間と言います。
時間の経過とともに故障発生率が低く安定してくると偶発故障(random failure) 期間「有効寿命」「耐用期間」とも呼ばれる)となります。
使用期間が長くなっていくと徐々に故障率が高くなっていき、偶発故障期間を過ぎると、磨耗故障 (Wear-Out failure)期間となります。
こうした概念モデルを知っておくことで、最適な分析手法を選択することが可能になります。
ポイント ①信頼性、保守性の検討に信頼性工学は欠かせない。
②信頼性工学には、さまざまな概念モデルがある。
③概念モデルからもっと有効な分析手法を選ぶ。
統計的検定の考え方
実験データーや市場調査データーの分析で2つのデーター群の間に「優位差があるかないか」を判断するケースがあります。
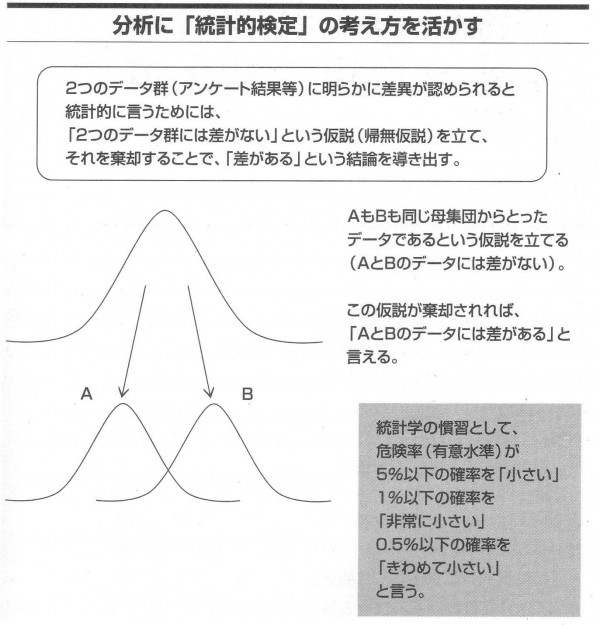
客観的に判定できるように多数のデーターを集めて、統計的な検定判断をすることになります。その際「AとBのデーター群には差がない」という仮説を立て、それが統計的に「違う」と高い確率で言えるかを検証します。
このような仮説はそれが違うと言いたい意図で作るものなので「帰無仮説」と呼ばれています。「AとBのデーター群には差がない」という仮説を棄却することで「AとBに差がある」というのが統計的検定の考え方です。
統計的検定ではどんなにデーターを増やしても100%の確率で仮説が間違っているとは言えません。5%の確率で判断を間違う可能性もあるが、おそらく「仮説は間違っている」と判断できるというように外れる確率を前提に検定します。この外れる確率は「危険率」「優位水準」などと呼ばれます。
誤りの発生には2種類の可能性があります。1つは本当は正しい仮説を少ないデーター量で判断して誤って棄却してしまう「あわてものの誤り」です。
もう1つは逆に本当は間違った仮説なのに多くのデーターをとっても間違いに気づかない「ぼんやりもの誤り」です。
誤解されていることが多いので注意が必要ですが、統計的検定で「AとBのデーターに差がない」という仮説を棄却できないと判断することは、「AとBのデーターに差がない」ということを強く肯定するものではありません。
「これだけでのデーターではAとBに差があるとは言い切れない」と言っているだけで「差がない」ことを証明しているわけではありません。
統計的検定の考え方は「疑わしきは罰せず。無罪と無実は必ずしも同じではない」という裁判の考え方と同じものなのです。
ポイント
①「差がある」というためには「差がない」仮説を立てる。
②「差がない」という仮説が棄却されることで「差がある」と判断する。
③帰無仮説が棄却されても「差がない」ことを証明しているわけではない。
回帰分析の考え方
アンケートなどで定量的に得られたデーターから意味ある情報を得る手法をいくつか紹介しましょう。
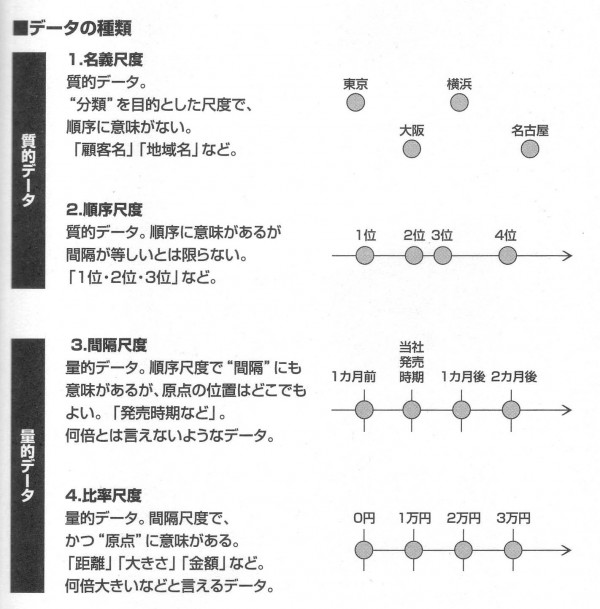
アンケートなどのデーターの種類には質的データー(名義尺度、順序尺度)と量的データー(間隔尺度、比率尺度) があります。
目的変数が量的変数なのか質的変数なのか、あるいは存在しないのかによって、利用する分析手法が異なります。
回帰分析
複数の説明変数から1つの目的変数を推定する分析手法です。たとえば、中古車の値段査定では、査定額が目的変数となり、年式、走行距離、次回の車検までの期間などのデーターが説明変数になります。 それぞれの説明変数が目的変数に与える影響度を計算で求め、目的変数を推定します。
判別分析
回帰分析と一部異なり、目的変数が質的変数(購入したい/したくないというような質的判断)になる場合に用いる分析法です。たとえば、商品のスペックの量的変数(値段、購入量、不良率等)が変わったときに、購入するか購入しないかの判断したデーターをもとに分析します。判断分析により、商品のスペックがそれぞれどう変化すると、購入されそうか否かの推定が可能になります。
主成分分析
データーに多くの定量データーが変数がある場合、これを1つの総合指標(合成変数)で代表させたい場合に 使う分析手法が主成分分析です。
たとえば、ある商品についていろいろな観点でお客さまの満足度評価データをもっている場合にそれらの複数の変数を1つの値で代表させて見たいときなどに使います。
参考文献: 問題を整理し、分析する技術 (株)日本能率協会コンサルティング